秒速で稼ぐという錯覚：統計が語る「秒」の危うさ

ツイッターなどでいわゆる「金融界隈」と呼ばれる方々の投稿を拝見するようになってから、少し気になることがあります。日々の相場を鋭く分析する方もいれば、短期売買の成果を誇る投稿も多く見られます。とりわけ、「デイトレードはリスクが少ない」「持ち越さないから安全」といった言葉を頻繁に目にするようになりました。確かに、オーバーナイトでポジションを保有しないという点では、翌日のニュースや金利変更といった外部ショックの影響を受けにくく、リスクが限定的に見えるかもしれません。しかし、実際の市場の動きや人間の心理を考えると、もう少し慎重に考える必要があります。SNS上には「デイトレードは安全」「秒速トレーダー」といった宣伝も見られますが、それは翌日にリスクを持ち越さないというだけであり、短期トレードには別の統計的なリスクが存在します。以下では、その「デイトレは安全なのか？」という前提について、少し掘り下げて考えてみたいと思います。

短期トレードのリスク構造：予測可能性の低下

時間軸が短くなるほど価格変動におけるノイズ比率が増大し、予測可能性は低下します。EUR/USDの年率ボラを日次から他の時間軸に換算する際には√Tが目安になりますが、超高頻度ではマイクロストラクチャー要因で単純な換算が崩れます。

投資期間	典型的1期間σ（EUR/USD）	取引コスト（片道bps）	情報比率の目安
1分	約0.02%	0.5–1.0	極めて低い（<0.1）
5分	約0.05%	0.5–1.0	低い（0.1–0.3）
1時間	約0.2%	0.5–1.0	やや低い（0.2–0.4）
1日	約0.5%	0.5–1.0	中程度（0.3–0.6）
1週間	約1.1%	0.5–1.0	やや高い（0.4–0.8）
1ヶ月	約2.3%	0.5–1.0	高い（>0.5）

出所：Andersen et al. (1998), Lyons (2001), Menkhoff et al. (2016) に基づく代表値。コストは機関投資家レベルの想定。リテールでは通常これ以上。

1分足では「標準偏差に対するコスト比率」が25–50%に達しやすく、ノイズに対してコストが大きすぎるため、統計的優位の確立が難しくなります。対照的に月次ではコストは標準偏差の0.2–0.4%程度にとどまります。

マイクロストラクチャー・ノイズ

• ビッド・アスク・バウンス（見かけ上のRV上振れ）
• 非同期取引（価格発見の遅延）
• 流動性の薄さ（板厚・約定確率の変動）

5分未満のサンプリングではRVが過大になりやすいことが知られており、測定上の歪みが実装段階ではスリッページやヒット率低下として顕在化します。

ここでいう「RV」は、Realized Variance（実現分散）の略です。RVは価格の高頻度データから計算される実際の価格変動の分散指標を指しています。 短期サンプリングではノイズが大きく、RVが過大に計測される（真のボラティリティより高く見える）点を論じています。 マイクロストラクチャー・ノイズの影響下では、観測される価格が「真の基礎価格」にランダム誤差を伴うため、短期サンプリングではRVが過大に計測されやすくなります。 これは市場構造の摩擦（スプレッド、約定遅延、取引非同期性）を反映する現象であり、短期トレードの再現性を低下させる主要因の一つです。

図：サンプリング間隔とRV（実現分散）の関係 ― マイクロストラクチャーノイズの影響

出典：dm13450.github.io（画像直リンク）。 サンプリング間隔を短くするほど、 マイクロストラクチャー要因により、RV（Realized Variance）が過大推定されやすい。 一方、間隔を長くするとノイズが平均化され、推定値が収れんしていく様子が視覚化されている。

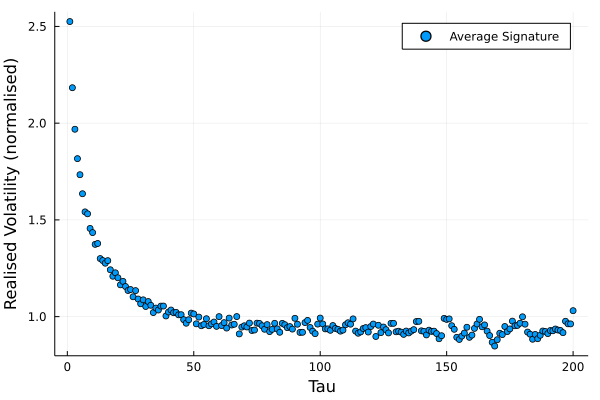
読み方：横軸はサンプリング間隔（秒〜分）、縦軸はRVの推定量（相対スケール）。 左端（短期）では観測ノイズの影響が強くRVが押し上がる。 右へ行くほどノイズが希釈され、真のボラティリティに近づく。 この記事の主張「短期ほどノイズ支配が強く、リスク指標が膨らみやすい」を視覚的に裏付ける。

• 短期：スプレッド起因の往復（バウンス）、非同期取引で相関が歪み、RV過大。
• 過渡域：ノイズと真の変動が混在、推定のばらつきが縮小。
• 長期：√t則に沿った安定化、推定が収れん。

自己相関の低さ：短期で予測が難しくなる理由

自己相関は、過去のリターンと現在のリターンの関連性を示す指標です。 高頻度（秒〜分）では、リターンの自己相関は短いラグで小さいが有意な負値になりやすく （主因はビッド・アスク・バウンスや在庫調整などのマイクロストラクチャ要因）、 ラグが数十秒〜数分を超えるとゼロ近傍へ急速に収束します。 このため、分足レベルの方向予測は統計的に困難になります。

自己相関係数 ρ(k) は k 時点前のリターンと現在のリターンの相関を表します。 超短期では ρ(1) が負になりやすい一方、少し時間軸を伸ばすと ρ(k) はゼロ近傍へ減衰します。

• 秒〜数分のラグで小さい負の自己相関が生じやすい（バウンス・在庫調整・非同期更新）。
• 数分以上では自己相関がゼロ近傍となり、予測決定係数 R² は極小に留まる。
• 高頻度アルゴが裁定機会を迅速に解消し、規則性の持続を妨げる。

観点	内容	影響
予測可能性の制約	超短期で ρ(1) は負、数分超でゼロ近傍へ収束	方向予測のR²が極小、勝率はコスト分だけ下振れ
シグナル劣化	短期テクニカルはノイズに埋没しやすい	当たり外れが増え、再現性が低下
マイクロ構造ノイズ	バウンス・非同期・板厚変動で短期RVが過大に見える	スリッページとヒット率低下としてコスト化

行動バイアス：デイトレが心理的に不利になる理由

人間の判断は必ずしも合理的ではありません。デイトレードのように短時間で繰り返し判断する環境では、 認知バイアスや感情的反応が強く影響し、取引成績を体系的に悪化させる傾向があります。 多くの研究は一般個人投資家を対象にしていますが、取引頻度の高い層はデイトレーダー的行動特性を示し、 結果はデイトレードにも統計的に適用できます。

主なバイアス	内容	デイトレへの影響
損失回避	利得より損失の心理的影響が大きい。Tversky & Kahneman (1992) は損失回避係数 λ ≈ 2.25 を推定。	損失ポジションを保持し、利益は早期確定。平均損益が逆転しやすい。
確証バイアス	自分のポジションに有利な情報を選択的に信じる傾向。	逆行時に損切りを遅らせ、誤った判断を補強する。
過信	自分の分析・勝率を過大評価しやすい（Barber & Odean, 2000）。	取引回数・レバレッジが増加し、手数料やスリッページの複利的負担が拡大。
ギャンブラーの誤謬	「そろそろ反発する／続落する」と確率を誤解する。	ランダムな連続値動きをトレンド転換と誤認し、反対売買を繰り返す。
近視眼的損益評価	短期損益を頻繁に確認し、ストレスや感情的判断が増える。	損益の変動に過敏に反応し、取引の一貫性が失われる。

関連研究とスコープ

以下の研究は、デイトレーダーを直接分析したものと、頻繁取引者を対象に行動バイアスを検証したものに分類できます。 後者の結果もデイトレ環境に統計的に整合します。

研究	対象	主な結果・示唆
Barber & Odean (2000, Journal of Finance)	米国個人投資家 約60,000口座（1991–1996）	最頻繁取引群の年率リターン11.4%、市場平均17.9%。差6.5%。過信とコスト累積が主因。
Odean (1998, Journal of Finance)	米国個人投資家 10,000口座	利益確定を急ぎ損失を保持するディスポジション効果を実証。 利益銘柄の売却確率は損失銘柄より高いが、「2倍」という定量は他研究（Grinblatt & Keloharju, 2001）に基づく。
Grinblatt & Keloharju (2001, JFQA)	フィンランド個人投資家パネル（1995–1996）	短期回転投資家のリターンは長期保有者より約5%低く、 moderate gainでの売却確率はmoderate lossの約2倍。
Barber, Lee, Liu & Odean (2009, Management Science)	台湾の個人投資家 約390万口座（1995–1999）	個人投資家全体で年平均GDP比約2.2%の損失。 上位1%のみが一貫して利益。デイトレ含む頻繁取引群は統計的にマイナス。
Jordan & Diltz (2003, FAJ) / Garvey & Murphy (2005, Financial Review)	米国NASDAQ・プロップデイトレーダー（1998–2000）	収益分布は右裾長で中央値は損失。利益は上位少数に集中。

これらの研究の多くはデイトレーダーを直接分析したものではありませんが、 頻繁取引者の行動構造（過信・損失回避・確証バイアス）はデイトレと同質です。 統計的には、取引頻度が上がるほど平均リターンは低下し、 行動バイアスがその主要因であることが確認されています。

HFTとの競争は不利

• レイテンシ優位（コロケーション、マイクロ波等）
• 板情報の高速解析
• 超回転で小さな優位を積み上げ

Menkveld (2013) は株式のMM型HFTについて1取引あたりの粗利が極小であることを示しています。FXとは市場構造が異なるものの、低マージン×高回転の構造は共通で、裁量デイトレがこの領域で対抗するのは現実的ではありません。

まとめ

デイトレが不利になる3要因

要因	説明	影響
取引コストの累積	スプレッド・手数料・スリッページが回転数に比例	年100回転で約100bps、年1000回転で約1000bps相当
自己相関の低さ	分足では予測R²が極小	テクニカル指標の有効域が限定
行動バイアス	頻回取引・損失回避・確証バイアス	個人投資家は頻繁取引ほど劣後しやすい

結論：デイトレは「安全」ではなく「翌日リスクを持たない」だけ。短期化するほど予測可能性は低下し、コストが相対的に重くなり、期待SRは悪化します。個人投資家が入りやすいのは、おそらくHFTの影響が少ない中長期の時間軸です。

---

参考文献

1. Andersen, T. G., and T. Bollerslev (1998). Deutsche Mark–Dollar Volatility: Intraday Activity Patterns, Macroeconomic Announcements, and Longer Run Dependencies. Journal of Finance 53(1): 219–265.
2. Andersen, T. G., Bollerslev, T., Diebold, F. X., and Labys, P. (2003). Modeling and Forecasting Realized Volatility. Econometrica 71(2): 579–625.
3. Barber, B. M., and T. Odean (2000). Trading is Hazardous to Your Wealth: The Common Stock Investment Performance of Individual Investors. Journal of Finance 55(2): 773–806.
4. Barber, B. M., Y.-T. Lee, Y.-J. Liu, and T. Odean (2009). Just How Much Do Individual Investors Lose by Trading? Review of Financial Studies 22(2): 609–632.
5. Burnside, C., Eichenbaum, M., Kleshchelski, I., and Rebelo, S. (2011). Do Peso Problems Explain the Returns to the Carry Trade? Review of Financial Studies 24(3): 853–891.
6. Cochrane, J. H. (2005). Asset Pricing, Revised Edition. Princeton University Press.
7. Dacorogna, M. M., Gençay, R., Müller, U., Olsen, R. B., and Pictet, O. V. (2001). An Introduction to High-Frequency Finance. Academic Press.
8. Della Corte, P., Riddiough, S. J., and Sarno, L. (2016). Currency Premia and Global Imbalances. Review of Financial Studies 29(8): 2161–2193.
9. Fama, E. F. (1970). Efficient Capital Markets: A Review of Theory and Empirical Work. Journal of Finance 25(2): 383–417.
10. Garvey, R., and A. Murphy (2005). Are Professional Traders Too Slow to Realize Their Losses? Financial Review 40(4): 423–445.
11. Grinblatt, M., and M. Keloharju (2001). What Makes Investors Trade? Journal of Finance 56(2): 589–616.
12. Jordan, D. J., and J. D. Diltz (2003). The Profitability of Day Traders. Financial Analysts Journal 59(6): 85–94.
13. Kahneman, D., and A. Tversky (1979). Prospect Theory: An Analysis of Decision under Risk. Econometrica 47(2): 263–291.
14. Lyons, R. K. (2001). The Microstructure Approach to Exchange Rates. MIT Press.
15. Menkhoff, L., Sarno, L., Schmeling, M., and Schrimpf, A. (2012). Carry Trades and Global Foreign Exchange Volatility. Journal of Finance 67(2): 681–718.
16. Menkhoff, L., Sarno, L., Schmeling, M., and Schrimpf, A. (2016). Information Flows in Foreign Exchange Markets: Dissecting Customer Currency Trades. Journal of Finance 71(2): 601–634.
17. Menkveld, A. J. (2013). High Frequency Trading and the New Market Makers. Journal of Financial Markets 16(4): 712–740.
18. Odean, T. (1998). Are Investors Reluctant to Realize Their Losses? Journal of Finance 53(6): 1775–1798.
19. Tversky, A., and D. Kahneman (1992). Advances in Prospect Theory: Cumulative Representation of Uncertainty. Journal of Risk and Uncertainty 5(4): 297–323.

注記：本稿の数値は主要通貨（EUR/USD）を念頭に置いた代表値。時期・通貨・流動性・口座属性・実装で大きく変動し、危機局面ではボラが数倍に上振れうる。実運用では自分のデータで検証すること。

---

付録：補足解説と実務的含意

自己相関の低さ：短期で予測が難しくなる理由

自己相関は、過去のリターンと現在のリターンの関連性を示す統計指標です。 高頻度（1分足・ティック）データでは、小さいが有意な負の自己相関が観測されるものの、 これは主にマーケットマイクロストラクチャーノイズ（ビッド・アスク・バウンス、在庫調整等）によるものです。 20秒から数分を超える時間スケールでは、この自己相関は消失し、 価格変動がランダムウォークに近い振る舞いを示すことが多くの研究で確認されています。 その結果、短期取引では方向性の予測が統計的に困難になります。

自己相関係数 ρ(k) は、k 分前のリターンと現在のリターンの相関を示します。 高頻度データでは、数秒から数分の短期間で負の自己相関（ρ(1) ≈ -0.05 ~ -0.15）が観測されますが、 これはビッド・アスク・バウンスや価格プレッシャーなどの一時的な効果によるものです。 20秒を超える時間スケールでは ρ(k) ≈ 0 となり、 過去の値が将来を説明しないことを意味します。

実証的特徴（主要研究）

• Andersen & Bollerslev (1997, 1998) は、為替市場の5分足データにおいて リターン自己相関が数値的に小さく（numerically small）、分散（ボラティリティ）のみが時間スケールに依存して変化することを確認。 論文の主眼はボラティリティの持続性と日中パターンの分析にあるが、 短期リターンの自己相関の小ささは副次的に報告されている。
• Dacorogna et al. (2001, An Introduction to High-Frequency Finance) によると、 FX・株式・債券いずれの市場でも、1分足レベルでは負の一次自己相関が観測される。 これは主にビッド・アスク・バウンス（取引価格がビッドとアスクの間で跳ね返る現象）や マーケットメイカーの在庫調整による一時的な価格プレッシャーが原因である。 高頻度では小さいが有意な自己相関構造があるものの、予測に利用できるほどの強さはない。
• 実証研究の一般的知見：10分足の株式リターンでは-0.09〜-0.15程度の 負の自己相関が観測される（米国株式市場、2006-2010年）。 この負の自己相関は、午後の取引時間帯（流動性取引が多い時間）により顕著であり、 朝の取引時間帯（情報取引が多い時間）では相対的に小さい。
• Cont et al. (2013) は、2010年のNYSE株式市場において、 20秒を超える時間スケールでは統計的に有意な自己相関が観測されないことを報告。 これは、マイクロストラクチャーノイズの影響が短時間で減衰することを示している。

自己相関が小さい・短命であると何が起こるか

観点	内容	影響
予測可能性の欠如	マイクロストラクチャーノイズを除けば、20秒以上のスケールで自己相関がほぼゼロとなり、過去データが将来を説明できない	方向予測モデルのR²が1%未満となり、勝率は50%に収束。数秒〜数分の負の相関もノイズ成分であり、取引コストで相殺される
シグナル劣化	移動平均・RSI・モメンタム系などのテクニカルシグナルが、高頻度ではマイクロストラクチャーノイズに埋もれる	短期では優位性が持続せず、取引回数に比例して手数料負担が増す
高頻度ノイズ	ビッド・アスク・バウンス、非同期約定、マーケットメイカーの在庫調整による価格プレッシャーが短期リターンに負の自己相関を生み出す	見かけ上のパターンは一時的で、スリッページやヒット率低下がコストとして顕在化。真の情報による価格変動と区別困難

統計的背景

短期リターンの自己相関の低さ（マイクロストラクチャーノイズを除去後）は、 効率的市場仮説（EMH） の短期的帰結でもあります。 情報が即座に価格へ反映されるなら、過去の価格から将来を予測する余地は残らないため、 数分以上の時間スケールではリターン系列が独立同分布（i.i.d.）に近づきます。 これはFama (1970, Journal of Finance) の理論的主張を、 高頻度データで実証した結果とも整合します。

ただし、秒単位から数分の超短期では、負の自己相関が観測されます。 これは市場の非効率性を示すものではなく、むしろマーケットメイキングの機能を反映しています。 マーケットメイカーは買い注文に対して在庫を売り、売り注文に対して在庫を買うことで流動性を提供しますが、 この在庫調整による価格プレッシャーは一時的なものであり、数秒から数分で解消されます。 したがって、この負の自己相関を利用した取引戦略は、取引コストとの競争になります。

時間スケールによる自己相関の変化

時間スケール	典型的な自己相関	主な要因
数秒〜数十秒	ρ(1) ≈ -0.05 ~ -0.15（負）	ビッド・アスク・バウンス、マーケットメイカーの在庫調整
1〜5分	ρ(1) ≈ -0.02 ~ -0.05（小さい負）	価格プレッシャーの残存効果
10分〜1時間	ρ(k) ≈ 0（ほぼゼロ）	ランダムウォーク的挙動、効率的市場
日次以上	弱い正または負（市場状況による）	モメンタム効果、リバーサル効果

実務的示唆

• 超高頻度での負の自己相関は取引可能か？ 理論的には数秒〜数分の負の自己相関を利用した平均回帰戦略が考えられるが、 実際にはスプレッド、手数料、スリッページなどの取引コストに吸収される。 HFT（高頻度取引）業者のみが、極めて低い取引コストとレイテンシーによって、 この領域での収益化が可能。
• モデル構築時の確認事項： 自己相関関数（ACF）が20秒〜数分で速やかにゼロへ減衰するかを確認する。 もし長期間にわたって自己相関が残存する場合、データの前処理（時間調整、非同期性の処理等）に問題がある可能性。
• 時間スケールの選択： ノイズ領域（数秒〜数分）を避け、ファンダメンタルや情報が影響する時間スケール（時間〜日単位）で分析する方が再現性が高い。 日次以上のデータでは、モメンタム効果やリバーサル効果など、より構造的なパターンが観測される。
• 分散（ボラティリティ）は予測可能： リターンの自己相関は低いが、リターンの二乗（分散、ボラティリティ）は 強い自己相関と長期記憶性を示す。これがGARCHモデルなどの ボラティリティ予測モデルが有効である理由。

統計的に有意な戦略の条件（目安）

実装ヒント

回転数とコストが大きいほど、必要SRは急増します。日次で年250回転・往復2bps程度なら必要SRはおおよそ0.3前後で現実的ですが、分足で年十万回転・往復2bpsでは必要SRは非現実的な水準になります。

実装チェックリスト

• 自分の実コスト系列を作成（時刻別スプレッド＋手数料＋スリッページ分布）
• 頻度別にσ・t統計・SRを比較（1分/5分/15分/1時間/日次）
• MS影響が強い時間帯や発表跨ぎを除外/別推定してロバスト性を確認
• 3–5年のOOSを確保し、現実のサイズでスリッページを再注入
• 約定ベースPnLと理論PnLの乖離を月次モニター（執行品質の劣化検知）

時間軸別の実務的含意

時間軸	予測可能性の源泉	典型的SRのレンジ
秒〜分	HFT裁定、MS効果	<0.1（裁量）
時〜日	センチメント、フロー偏り	0.2–0.4
週〜月	金利差、RP、マクロ	0.4–0.8
四半期〜年	金融政策、PP偏差の是正	0.5–1.0

出所：Burnside et al. (2011), Menkhoff et al. (2012), Della Corte et al. (2016)。レンジは代表値であり、戦略・時期で変動。